聚类是一种无监督分类,K-均值聚类可以在训练数据集中发现K个不同的簇,且每个簇的中心采用簇中所含训练数据的均值计算而成。
K-均值聚类算法
优点:简单,容易实现。
缺点:可能收敛到局部最小值,在大规模数据集上收敛较慢。
K-均值算法的工作流程为:首先,确定 $k$ 个初始点作为质心;然后将数据集中的每个点分配到相应的簇中,准确的说,就是在数据集中,为每个点计算其到各个质心的距离,并将数据点分配给距离最小的质心。完成后再更新质心为该簇的平均值。
上述过程伪代码描述如下:
$\qquad$创建 $k$ 个点最为初始质心(通常随机选择)
$\qquad$当任意一个点的簇分配结果发生改变时:
$\qquad\qquad$遍历数据集,对每个点:
$\qquad\qquad\qquad$对每个质心:
$\qquad\qquad\qquad\qquad$计算数据点到质心的距离
$\qquad\qquad\qquad$将数据点分配给距离最近的质心
$\qquad\qquad$对每一个簇,计算该簇中所有数据点的均值作为质心
使用后处理来提高聚类性能
K-均值算法收敛但聚类效果较差的原因就是收敛到局部最小值,而非全局最小值。一种用于度量聚能效果的指标是SSE(Sum of Squared Error,误差平方和)。聚类的目标是在保持簇数目不变的情况下提高簇的质量。
有两种可以量化的方法:合并最近的质心,或者合并两个使得SSE增幅最小的质心。第一种思路需要计算所有质心之间的距离,然后选择距离最小的两个质心合并来是实现;第二种思路需要合并两个簇然后计算总SSE值。这必须在所有可能的两个簇上重复该过程,找出最佳的两个簇。
二分K-均值算法
为了克服K-均值算法收敛与局部最小值的问题,提出了一种称为二分K-均值算法。该算法首先将整个数据集作为一个簇,然后将该簇一分为二,之后选择其中的一个簇继续进行划分。选择哪一个簇进行划分取决于该划分是否最大程度降低SSE值。上述基于SSE的划分过程不断重复,直到满足指定的簇数。该过程伪代码描述如下:
$\qquad$将整个数据集看成一个簇
$\qquad$当簇的数目小于 $k$ 时:
$\qquad\qquad$对于每一个簇:
$\qquad\qquad\qquad$计算总误差
$\qquad\qquad\qquad$将给定的簇进行K-均值聚类(k=2)
$\qquad\qquad\qquad$计算将簇一分为二后的总误差
$\qquad\qquad$选择使得误差最小的那个簇进行划分操作
实验(python实现)
附:数据集下载链接:http://pan.baidu.com/s/1eRzQTAM
效果图: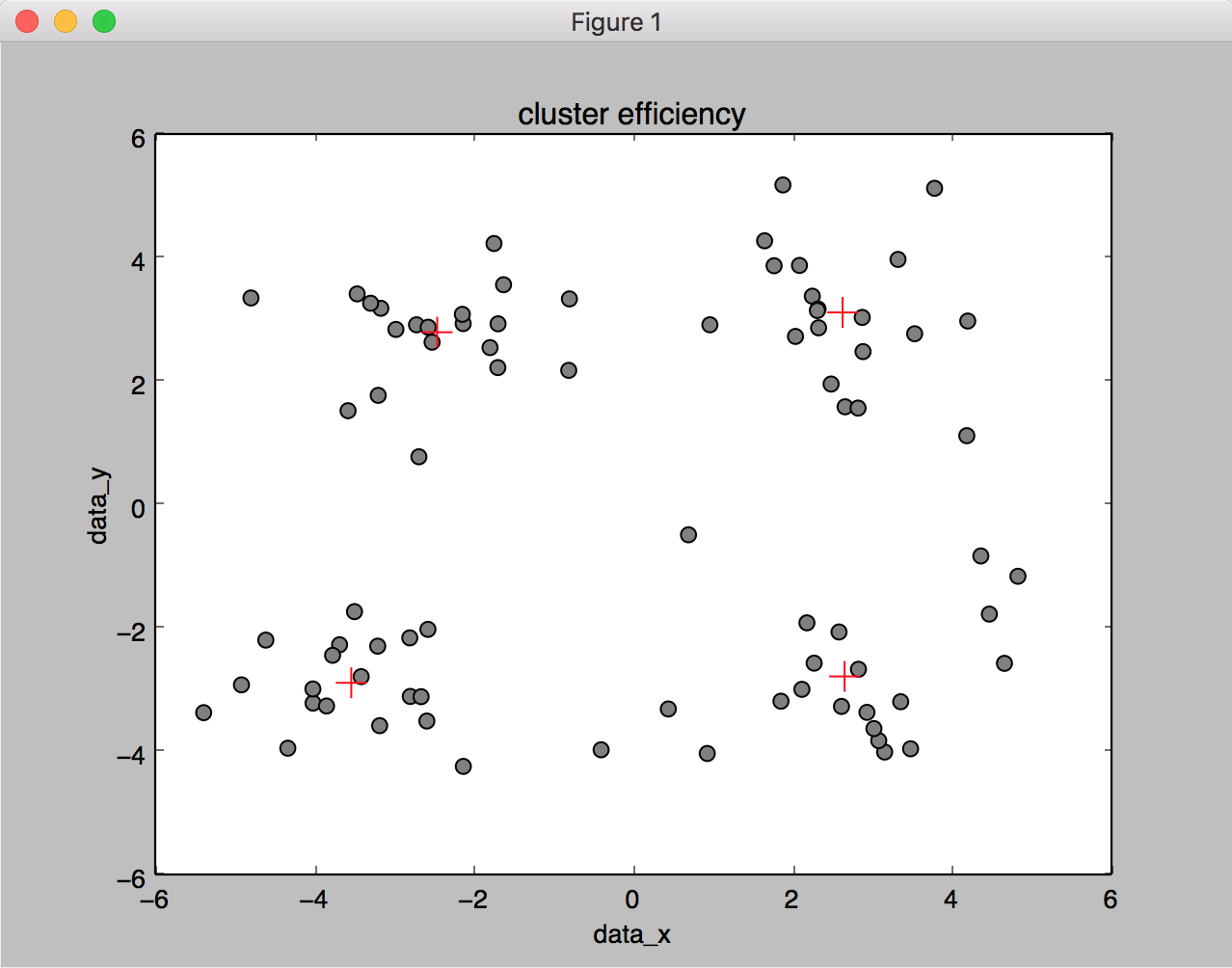
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112# -*- coding: UTF-8 -*-
import numpy as np
import math
import matplotlib.pyplot as plt
# 读取数据集
def load_dataset(file_path):
dataset = []
fr = open(file_path)
for line in fr.readlines():
line_arr = line.strip().split('\t')
line_float = map(float, line_arr)
dataset.append(line_float)
fr.close()
return dataset
# 计算距离
def get_distEuclidean(vecA, vecB):
return math.sqrt(np.sum(np.power(vecA - vecB, 2)))
# 随机生成簇的质心
def get_randCenter(dataset, k):
n = dataset.shape[1]
centroids = np.mat(np.zeros((k, n)))
for j in range(n):
minJ = min(dataset[:, j])
rangeJ = float(max(dataset[:, j]) - minJ)
centroids[:, j] = minJ + rangeJ * np.random.rand(k, 1)
# centroids = np.mat('-0.27409069 4.06949785;-4.46276867 -0.79273077;-2.65375091 -4.00954913;-4.53611874 4.14258773')
return centroids
# 普通的k-均值聚类
def k_means(dataset, k):
m = dataset.shape[0]
cluster_assment = np.mat(np.zeros((m, 2))) # 与数据集相对应,第一列保存簇,即类别,第二列保存距离,即数据到质心的距离
centroids = get_randCenter(dataset, k) # 初始化k个质心
cluster_changed = True
while cluster_changed:
cluster_changed = False
for i in range(m): # 遍历数据集
min_j = -1
min_dist = np.inf
for j in range(k): # 遍历质心,寻找最短距离
dist = get_distEuclidean(dataset[i, :], centroids[j, :])
if min_dist > dist:
min_dist = dist
min_j = j
if cluster_assment[i, 0] != min_j:
cluster_changed = True
cluster_assment[i, :] = [min_j, min_dist ** 2] # 更新第i个数据对应的质心和与质心的距离
# print centroids
for cent in range(k):
class_cent_list = (cluster_assment[:, 0].A == cent).nonzero()[0]
centroids[cent, :] = np.mean(dataset[class_cent_list], axis=0)
return centroids, cluster_assment
# 二分k-均值聚类
def bipartite_k_means(dataset, k):
m = dataset.shape[0]
cluster_assment = np.mat(np.zeros((m, 2))) # 第一列保存所属的簇,第二列保存与该簇质心的距离
centroid_0 = np.mean(dataset, axis=0).tolist()[0] # 初始化整个数据集为一簇时的质心
centlist = [centroid_0] # 保存所有质心
for i in range(m): # 遍历数据集,计算样本点到质心的距离
cluster_assment[i, 1] = get_distEuclidean(dataset[i, :], centroid_0)
while len(centlist) < k:
min_SSE = np.inf
for i in range(len(centlist)): # 遍历已经聚类的簇
dataset_curr_cluster = dataset[(cluster_assment[:, 0].A == i).nonzero()[0], :] # 将第i簇的数据集提取出来单独处理
centroid_i, cluster_split = k_means(dataset_curr_cluster, 2)
SSE_split = sum(cluster_split[:, 1])
SSE_non_split = sum(cluster_assment[(cluster_assment[:, 0].A != i).nonzero()[0], 1])
if (SSE_split + SSE_non_split) < min_SSE:
min_SSE = SSE_non_split + SSE_split
minSSE_centroid_index = i # 记录使得误差平方和最小时的划分的母簇的序号
minSSE_cluster_split = cluster_split.copy() # 保存使得误差平方和最小时的划分的两个子簇数据集到各自质心的距离
minSSE_centroid = centroid_i # 保存使得误差平方和最小时的两个子簇的质心
# 两个子簇在放入总的centlist前,需要将其簇序号分别设为centlist最后一个和当前分解的这个一边替换
minSSE_cluster_split[(minSSE_cluster_split[:, 0].A == 1).nonzero()[0], 0] = len(centlist)
minSSE_cluster_split[(minSSE_cluster_split[:, 0].A == 0).nonzero()[0], 0] = minSSE_centroid_index
cluster_assment[(cluster_assment[:, 0].A == minSSE_centroid_index).nonzero()[0], :] = minSSE_cluster_split # 替换
centlist[minSSE_centroid_index] = minSSE_centroid.tolist()[0] # 将分解得到的子簇添加到centlist中
centlist.append(minSSE_centroid.tolist()[1])
return centlist, cluster_assment
# 图形化展示结果
def plot_centroids(dataset, centroids):
fig = plt.figure()
ax = fig.add_subplot(111)
dataset_x = dataset[:, 0].tolist()
dataset_y = dataset[:, 1].tolist()
ax.scatter(dataset_x, dataset_y, marker='o', s=50, c='gray')
centroids_x = centroids[:, 0].tolist()
centroids_y = centroids[:, 1].tolist()
ax.scatter(centroids_x, centroids_y, marker='+', s=200, c='red')
plt.title('cluster efficiency')
plt.xlabel('data_x')
plt.ylabel('data_y')
plt.show()
if __name__ == '__main__':
k = 4
dataset = load_dataset("testSet.txt")
centroids, cluster_assment = bipartite_k_means(np.mat(dataset), k)
plot_centroids(np.mat(dataset), np.mat(centroids))